강화학습을 공부할 때 Policy gradient 라는 말을 종종 듣게 된다.
예를 들면, 강화학습 기법 중 Policy gradient 계열로는 A2C, PPO 등이 있고, 이들은 on-policy 방식이다. 등등.
policy gradient 라는건 단순히 '정책'의 '경사도'라 볼 수 있으나,
좀 더 자세히 알아보자.
일단 지피티에게 대충 물어보면...
이 질문 진짜 핵심이에요.
강화학습에서 자주 등장하는 Policy Gradient 기법의 "gradient"가 뭔지 정확히 이해하면, 왜 이런 방식으로 정책을 업데이트하는지 흐름이 잡히거든요.
📌 여기서 gradient란?
Gradient(그래디언트) 는 수학적으로 기울기, 즉 함수의 증가/감소 방향과 크기를 나타내는 값이에요.
여기서 사용하는 gradient는
👉 정책의 파라미터(θ)에 대한 기대 보상의 기울기
즉,
“현재 정책의 파라미터 θ를 어느 방향으로 얼마나 바꿔야 기대 보상 $J(\theta)$ 가 커지는지 알려주는 값”
이라는 뜻이에요.
즉, gradient는 기울기를 말하는데, policy gradient는 정책의 파라미터에 대한 기울기로서, 파라미터를 어느 방향으로 바꿔야 보상이 커질 것인가? 라는 질문에 답이라는 뜻이다.
📌 그럼 Policy Gradient란?
정책을 직접 최적화하기 위해
정책의 파라미터를 기대 보상을 기준으로 gradient ascent (기울기 상승법)을 통해 업데이트하는 방법이에요.
수식으로 표현하면:
$$\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)$$
여기서
- θ\theta: 정책 파라미터
- α\alpha: 학습률
- ∇θJ(θ)\nabla_{\theta} J(\theta): 정책 파라미터에 대한 기대 보상의 gradient
즉, 보상을 많이 주는 방향으로 정책을 조금씩 수정해나가는 거죠.
정리하면, 강화학습을 이용해서 보상을 더 많이 받을 수 있는 쪽으로 정책을 최적화 하려는데, 아예 정책의 기울기를 이용해서 정책을 직접 최적화 하는 방법을 말한다. 참고로 Policy Gradient 방식이 아닌 걸로, DQN이 있는데, DQN은 정책을 직접 최적화 하는 방식(Policy Gradient)방식이 아니라, Q-Learning을 이용해서 행동(Action) 데이터를 많이 쌓아서 정책을 최적화 하는 방식을 사용한다.
📌 Policy Gradient의 대표 공식 (REINFORCE)
가장 기본적인 Policy Gradient 알고리즘인 REINFORCE의 gradient 추정 식:
$$\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(a|s) \cdot G_t \right]$$
여기서
- $\log \pi_{\theta}(a|s)$: 현재 정책이 해당 행동을 선택할 확률의 로그
- $G_t$: 해당 행동 이후 얻는 총 보상 (return)
→ 확률적으로 좋은 행동(보상을 많이 준 행동)은 그 확률을 높이고, 나쁜 행동은 확률을 줄이도록 정책을 조정
이걸 gradient ascent로 반복
오케. 대충은 알겠다. 그런데 머리로 이해하는 것만 하지 말고 실제 예제를 한번 보자.
import gymnasium as gym
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical
# 간단한 정책 네트워크 정의
class PolicyNetwork(nn.Module):
def __init__(self):
super(PolicyNetwork, self).__init__()
self.fc = nn.Sequential(
nn.Linear(4, 128), # CartPole observation 4개
nn.ReLU(),
nn.Linear(128, 2), # 행동 2개 (좌/우)
nn.Softmax(dim=-1)
)
def forward(self, x):
return self.fc(x)
# 환경 설정
env = gym.make("CartPole-v1", render_mode='human')
policy = PolicyNetwork()
optimizer = optim.Adam(policy.parameters(), lr=0.01)
# 하이퍼파라미터
num_episodes = 500
gamma = 0.99 # 할인율
# REINFORCE 학습 루프
for episode in range(num_episodes):
state, _ = env.reset()
log_probs = []
rewards = []
done = False
while not done:
state_tensor = torch.tensor(state, dtype=torch.float32)
probs = policy(state_tensor)
dist = Categorical(probs)
action = dist.sample()
log_probs.append(dist.log_prob(action))
state, reward, done, _, _ = env.step(action.item())
rewards.append(reward)
# 리턴 계산 (G_t)
returns = []
G = 0
for r in reversed(rewards):
G = r + gamma * G
returns.insert(0, G)
returns = torch.tensor(returns)
# 리턴 정규화 (학습 안정화)
returns = (returns - returns.mean()) / (returns.std() + 1e-9)
# Policy Gradient 계산 및 업데이트
loss = []
for log_prob, G in zip(log_probs, returns):
loss.append(-log_prob * G)
loss = torch.stack(loss).sum()
optimizer.zero_grad()
loss.backward()
optimizer.step()
if episode % 10 == 0:
print(f"Episode {episode}, total reward: {sum(rewards)}")
env.close()
위의 코드를 실행하면 아래와 같은 결과와 화면을 얻을 수 있다.

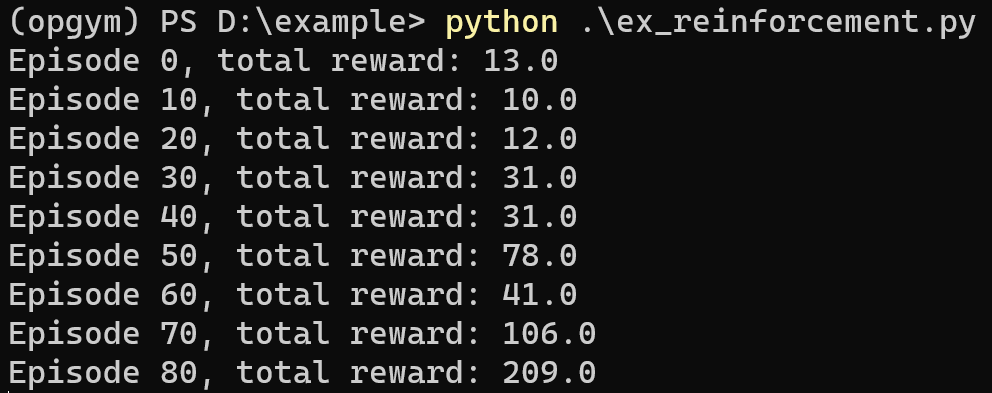
Episode가 늘어날 수록 더 높은 reward를 획득하는 것을 볼 수 있다.
코드 중간에 아래와 같은 계산부가 있다.
# Policy Gradient 계산 및 업데이트
loss = []
for log_prob, G in zip(log_probs, returns):
loss.append(-log_prob * G)
loss = torch.stack(loss).sum()이 부분이 위에 있는 수식
$$\nabla_{\theta} J(\theta) = \mathbb{E}_{\pi_{\theta}} \left[ \nabla_{\theta} \log \pi_{\theta}(a|s) \cdot G_t \right]$$
에 해당하는 부분이다.
전체 구조를 기억해두면 다음에도 비슷한 구조가 나와서 도움이 될 것이다.
그럼 이만~~
'Deep Learning' 카테고리의 다른 글
| 강화학습 on-policy vs off-policy (0) | 2025.05.23 |
|---|---|
| Imitation Learning에서 DQN 으로. (0) | 2025.05.21 |
| Gymnasium (강화학습 라이브러리) (0) | 2025.05.20 |
| Imitation Learning - gymnasium (0) | 2025.05.19 |
| Classification with unknown (1) | 2025.05.18 |

